OpenMusic Reference

accumulator

(control module) -- a general-purpose collector for the omloop function

Syntax

accumulator accum init fun &optional retard

Though it is called accumulatoor in its LISP code, this function appears as acum when used inside omloop . The reason eludes me.

—|—

Inputs

Output

Description

accumulator is part of a group of functions for performing iterative loops. They can only be used within an omloop patch window. Since they only function within the context of the entire repeating loop, they (or any function connected to them) cannot be evaluated directly within the patch window. You must evaluate the entire loop. See the entry on omloop for more information.

—|—

accum is is the most general type of collector. For each repetition of the loop, accumulator takes the value at the first input and a value previously stored in its register and passes them both to the lambda function or patch specified at the third input. The resulting value is stored in the register and the loop repeats.

Like all collectors, listing has three outputs:

The first output triggers the collector, evaluating whatever is connected to it and calling function fun as described above. It is usually connected to eachTime . The value carried by the connection itself is the current result of the evaluation of the loop, which you can test by placing the LISP function print between the first output and eachTime .

The second output returns the current state of the collector, without evaluating whatever is connected to it. It is usually connected to finally so that you can get the results of the collection.

The third output reinitializes the collector, resetting it to whatever value you specified at the init input. It will always return this value.

Examples

accum is the most generalized type of collector. Some collectors are special versions of the accumulator function. In these cases, the example of the use of the specific collector is reproduced with accumulator to illustrate this. You can therefore refer to the entries for the other accumulators for more examples of its use.

Using accumulator to add up a list of values

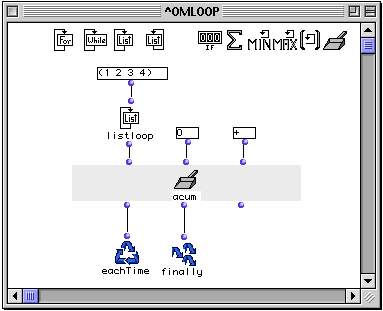
This example takes the sum of the elements (1 2 3 4). It returns:

? OM->10

Here’s how this happens: at each repetition of the loop, the output of listloop , which is stepping through the elements of the list one at a time, is passed to the function + , along with the value of the internal state of the accumulator. The internal state is simply the value stored by the accumulator at the end of the previous loop. If it is the first iteration (there was no previous loop) then the internal state is the value specified at the second input. The result of + becomes the internal state for the next loop. On each repetition, either eachTime or finally is evaluated. eachTime is evaluated on all but the last repetition, causing the accumulator to evaluate its function at the third input. On the last repetiton, finally is evaluated, which simply returns the internal state of accumulator . This is presented in the table below, which shows values after each loop.

Loop	Output of listloop (Value at the First Input of accumulator )
Internal State of accumulator	Output of binary function +
1	1	0	1
2	2	1	3
3	3	3	6
4	4	6	10
			10

On the last repetition, the value of the internal state is returned: 10

Making nested lists with accumulator

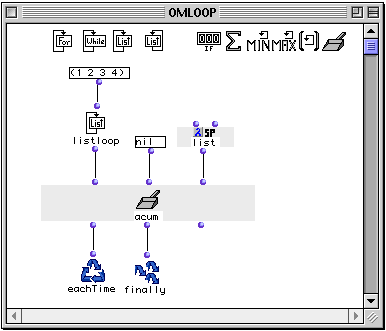
We will set up accumulator with the LISP function list instead of + . The other inputs are unchanged. The processing of the data is summarized below:

Loop	Output of listloop (Value at the First Input of accumulator )
Internal State of accumulator	Output of binary function list
1	1	nil	(nil 1)
2	2	(nil 1)	((nil 1) 2)
3	3	((nil 1) 2)	(((nil 1) 2) 3)
4	4	(((nil 1) 2) 3)	((((nil 1) 2) 3) 4)
			((((nil 1) 2) 3) 4)

Approximating π* with accumulator

This example is based on a formula discovered by French mathematician Jacques Bernoulli (1654-1705). The formula calculates π The square root of the sum of an infinite series of fractions where the denominators are squares of the integers, multiplied by 6: (remeber that the notation a^b means a to the bth power)

π = (6 (1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 +…))^.5

Calculating this series out to a greater length gives a more accurate estimation of π.The terms of the series, namely one over the square of an integer, and their sum can be represented by the following patch:

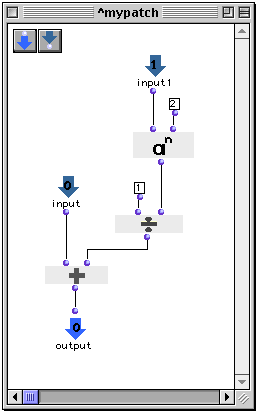
The input 1 will be an integer, which will be squared, and used to divide one. The result will be added to input 0, which will be the internal state of the accumulator. This patch, mypatch , is connected in lambda mode to the third input of accumulator . The second input is set to one (setting it to zero would cause a division-by-zero error in the first iteration of the loop) and the first input takes the output of a forloop , which will tick off the integers between 2 and 500, inclusive (we didn’t do 1 to 500 because the accumlator is already initialized to 1)

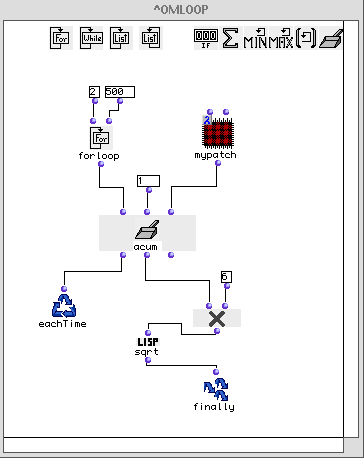
At each repetition, the number from forloop is passed to mypatch along with the internal state, and the result becomes the new internal state. This calculates the repeating, infinite series at the heart of Bernoulli’s equation. After the series has been calculated, all that remains is to multiply it by 6 and take the square root. This is post-processing. Note that is performed by functions inserted between the second output of accumulator and finally .

As we said, extending the series gives a more accurate result. With 500 steps, this loop returns:

? OM->3.139684123138722

With 5000 steps, the result becomes more accurate:

? OM->3.141401680950935

This example is to demonstrate the use of a patch in lambda mode with accumulator . There is a much easier way to get π. If you just wanted π for a calculation, it would be better to use the function eval with the constant pi :

About pi

π or pi, is the ratio of the circumference of a circle to its diameter it is an irrational number, meaning that it is a number with decimal places that do not repeat in any discernable pattern, ever. It thus cannot be represented by a finite series of numbers. The first ten decimal places of π are: 3.1415926535… and it just keeps going!

Prev	Home	Next
listing	Up	loopdo (eachTime)

OpenMusic

Visual Programming | Computer-Assisted Composition