OpenMusic Reference
approx-m

approx-m
(conversions module) -- rounds off midics to fit whole-number divisions of the octave
Syntax
approx-m midic approx &optional ref-midic
Inputs
| name | data type(s) | comments |
|---|---|---|
| midic | an integer or list thereof | the midics to round off |
| approx | a positive number | the subdivision of the octave to respect; defaults to 2. Note that decimal values are allowed |
| ref-midic | an integer | optional; specifies a reference pitch, as a midic |
Output
| output | data type(s) | comments |
|---|---|---|
| first | an integer or list thereof |
Description
This function accepts either a midic value or a list of midic values at its first input. They will be rounded off to their nearest note in an equal-tempered subdivision of the octave. This subdivision is specified at the second input. The octave of 1200 midics will be subdivided into ( approx *6) equal parts, and the values of midic will be rounded to these numbers. The default value of 2 for approx produces a traditional twelve-tone octave. 1 will produce a whole-tone, 6-step subdivision. 4 will produce a quarter-tone, 24-step division, and 8 will produce an eighth-tone, 48-step division of the octave. Other integers may be entered if desired do divide the octave in other ways.
The optional ref-midic input allows you to specify a reference pitch, in midics. This pitch will be subtracted from all the midics before the approximation is performed, and the resulting pitch or list will thus be relative to this midic.
Examples
Converting a fibonacci series to midics with approx-m
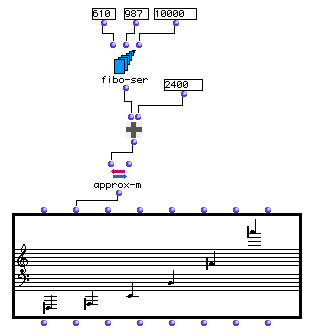
Here we turn a fibonacci series into a melodic line. The fibo-ser function will return the elements of the fibonacci series starting with 610 and 987 and running through 6765: (610 987 1597 2584 4181 6765)
We will consider these values as midics. We add 2400 to these values (transposing them up 2 octaves), yielding (3010 3387 3997 4984 6581 9165). Then we pass them to approx-m , which rounds them to semitones by default:
? OM->(3000 3400 4000 5000 6600 9200)
We now have a list of midics rounded off to the nearest semitone, which we can process in other ways. We can visualize them by plugging them into the second input of a Chord-seq object. Note that the **Chord-seq object always displays its midics rounded off to nearest semi-, quarter-, or eighth-tone. If our goal was simply to visualize the pitches, we could have plugged the om+ results directly into the second input of Chord-seq.**
| Prev | Home | Next |
|---|---|---|
| apply | Up | arithm-ser |