OpenMusic Reference
geometric-ser

geometric-ser
(series module) -- generates a geometric series
Syntax
geometric-ser seed factor limit &optional nummax begin end
Inputs
| name | data type(s) | comments |
|---|---|---|
| seed | a number | the starting point of the series |
| factor | a number | the multiplicative coefficient of the series |
| limit | a number | the upper limit of the series |
| nummax | a non-zero integer | optional; the maximum number of terms produced. Defaults to 10 |
| begin | a non-negative integer | optional; the ordinal of the first term to take |
| end | a non-negative integer | optional; the ordinal of the last term to take |
Output
| output | data type(s) | comments |
|---|---|---|
| first | a list |
Description
Returns a geometric series. An geometric series is a series in which the next term is produced by multiplying the previous term in the series by a fixed number.
gemoetric-ser produces a list of terms starting at seed and produces new terms by multiplying each successive term by factor until the series reaches limit or would exceed limit in its next term.
The optional input nummax allows you to limit the number of terms in the series. When it is set, the series will have a maximum of ( nummax plus 1) terms. It will still end on or before end , however.
Additionally, you can specify two optional inputs begin and end , which will cause geometric-ser to return only the range of elements of the series between the two inputs.
When limit , nummax , begin and end specify different ending points for the series, the priority for determining the length of the list is given first by limit , then the terms between begin and end , and then with nummax .
Examples
Limiting the range of a geometric series with geometric-ser
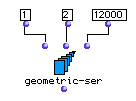
Here we see geometric-ser set to produce a series of powers of 2 stopping at or before reaching 12000. It returns
? OM->(1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192)
Setting nummax to 10, we limit the series to 11 elements, even though limit is set to 12000:
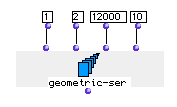
it returns:
? OM->(1 2 4 8 16 32 64 128 256 512 1024)
Finally, if we set begin to 8 and end to 11, we get only the 7th through 10th elements of the series:
? OM->(256 512 1024 2048)
| Prev | Home | Next |
|---|---|---|
| funcall | Up | get-chords |