OpenMusic Reference
samplefun
samplefun
(functions module) -- samples a function’s output at defined intervals
Syntax
samplefun fun step &optional xmin xmax coeff
Inputs
| name | data type(s) | comments |
|---|---|---|
| fun | a function name or lambda function | the function to sample |
| step | a positive number | the interval between samples; defaults to 1 |
| xmin | a number | optional; the beginning of the range of values for which to sample fun ; defaults to 0 |
| xmax | a number | optional; the end of the range of values for which to sample fun ; defaults to 10 |
| coeff | a number | optional; the results of the sampling are multiplied by this coefficient; defaults to 1. |
Output
| output | data type(s) | comments |
|---|---|---|
| first | a list | containing samples of function fun ‘s output |
| second | a BPF object | can be plugged directly into a BPF to display the sampled values graphically |
Description
samplefun passes a series of values to a function returns the results, either in a list or displayed graphically in a BPF object.
The a range of values between xmin and xmax are passed sequentially to fun . The results are multiplied by coeff and collected as the output. The first value is xmin After that, step is added to xmin and the result is passed to fun . This, continues, augmenting the value passed each time by step , up to the value specified at xmax .
The values can be taken directly at the first output in a list, or read as a BPF object at the second output. The scales of the axes of the BPF are adjusted automatically so that the entire range of values fits on the screen.
Examples
Graphing a sine wave
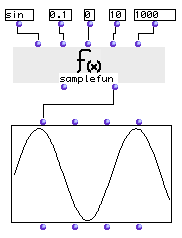
Here we graph a sine wave. The function sin is given the values bewtween 0 and 10 (the defaults, see warning) by increments of .1 (i.e. 0, .1, .2, .3 etc.). The results are multiplied by coeff , which defaults to 1000; again, see warning. Multiplying the values by 1000 makes them display better in the BPF since the BPF rounds off values to no decimal places by default and this would destroy the curve. The results are returned in a list (are you ready?):
? OM->(0.0 99.83341664682816 198.66933079506126 295.5202066613396 389.4183423086505 479.425538604203 564.6424733950354 644.217687237691 717.3560908995227 783.3269096274832 841.4709848078965 891.2073600614353 932.0390859672262 963.5581854171929 985.4497299884603 997.4949866040545 999.5736030415051 991.6648104524686 973.847630878195 946.3000876874144 909.2974268256814 863.2093666488735 808.4964038195898 745.7052121767197 675.4631805511503 598.4721441039558 515.5013718214634 427.379880233829 334.98815015590384 239.24932921398113 141.1200080598659 41.580662433289156 -58.374143427581416 -157.74569414324995 -255.54110202683293 -350.7832276896215 -442.5204432948541 -529.8361409084948 -611.8578909427207 -687.7661591839754 -756.8024953079295 -818.2771110644113 -871.5757724135887 -916.1659367494552 -951.6020738895161 -977.530117665097 -993.6910036334644 -999.9232575641008 -996.1646088358408 -982.4526126243328 -958.924274663139 -925.8146823277331 -883.4546557201545 -832.2674422239027 -772.7644875559894 -705.5403255703944 -631.2666378723244 -550.6855425976413 -464.6021794137613 -373.876664830241 -279.415498198931 -182.16250427210113 -83.0894028175026 16.813900484343495 116.54920485048659 215.1199880878086 311.5413635133711 404.849920616591 494.1133511386012 578.4397643881929 656.9865987187824)
This kind of data is not very approachable. Connecting the second output to a BPF object and evaulating that makes the data visual. The result is shown above; the sine wave is clearly visible.
Visualizing the results of a lambda function
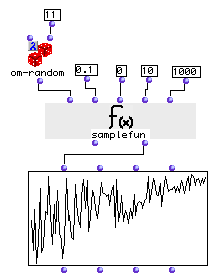
Here’s an example of connecting a function in lambda mode and visualizing the results through the bpf output. The function om-random returns random numbers between the values specified at its two inputs. The second input is set to 11. The first input will be the values passed by samplefun . We can see from the inputs that they will start at 0 and run through 10 by increments of .1. As they rise, the possible range of values returned by om-random will get smaller; this trend is clearly visible in the BPF.
| Prev | Home | Next |
|---|---|---|
| rotate | Up | save-as-etf |