OpenMusic Tutorials

Prev| Chapter 7. Breakpoint Functions| Next

Tutorial 21: Using BPFs III: Scaling a melodic

contour

Topics

Scaling a melody to fit within a given interval

Key Modules Used

BPF, bpf-sample, first, om-scale, om-round

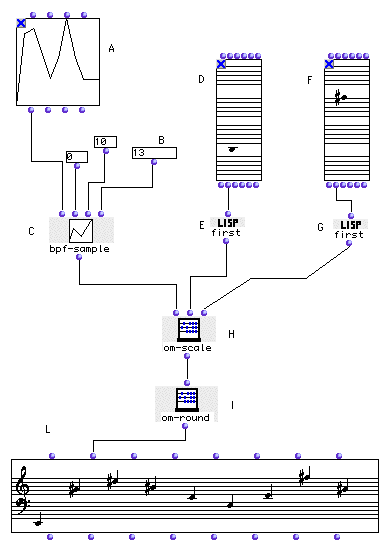
The Concept:

Here we start with a BPF object. We sample it at as many points as we like with the bpf-sample to create a contour with n elements (in this case, 13). These points are then scaled with om-scale to occur within the interval specified at its _minout_ and _maxout_ outputs. We set these numbers using midic outputs of Chord objects; the result is that the melodic form occurs between the two extremes.

The Patch:

Open the BPF:

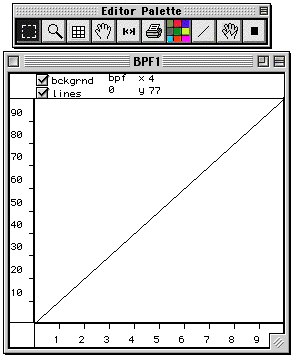
Here’s a graphic editor for BPF objects. You add new points to the graph by using the Add Points Tool:

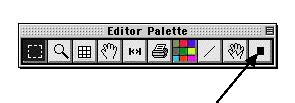
…and clicking on the graph. If you make a mistake, use the Select Points Tool (first on palette) and select the points by clicking or dragging, then hit delete.

Open the Chord box (D) and enter one note. The note you enter will be the lowest note of your melodic profile.

Open the Chord box (F) and enter one note. The note you enter will be the highest note of your melodic profile.

The midic outputs of the Chord objects give a list of midics. Even though they only contain one note, they still return that midic in parentheses, a list of one element. To isolate this atom (single element) of the list, we use first, which takes the first (and only) element of these lists. These midic values are passed to om-scale, which adjusts the list at its first input such that the relative distance between elements stays the same but the highest and lowest values come out to be the inputs _minout_ and _maxout_.

Note that the om-round box is technically superfluous; we could have entered the result of om-scale directly into the Chord-seq, which rounds pitches off for display anyway. It does, however, make the pitches easier to read for humans. Compare the output of the om-scale function with the output of om- round.

OpenMusic