OpenMusic Tutorials
Prev| Chapter 13. Flow Control III: More Loops!| Next
Tutorial 37: Accumulation with musical objects
Topics
Given a starting note and a melodic sequence, construct a random sequence of
notes with the same intervals as the melodic sequence but random directions of
motion. Use of a lambda patch within omloop with
acum.
Key Modules Used
omloop, Note, Chord-seq, x->dx, om-random,
om=, omif
The Concept:
Given a sequence of intervals (B) we will construct a musical sequence
starting from a given note (A). The intervals will be ordered as defined but
their direction (up or down) will be random (i.e ascending or descending
depending on om-random’s output). In order to do so we
will use an accumulative proceedure using omloop’s
acum collector.
We will also demonstrate the sequence function by
simultaneously visualizing our new melodic figure using a
BPF factory.
The Patch:
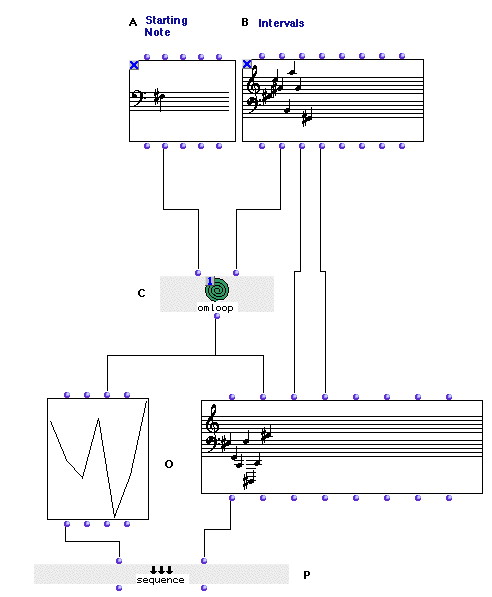
The transformation of the sequence into a new one will be done in
omloop (C). This transformation is a transformation of pitch
only, so omloop (C) is connected to the second input of
Chord-seq (O). To get the rhythmic data we take the
_ldur_ and _lonset_ outputs of the Chord-seq (B) and
copy them directly.
omloop as shown above is in ‘eval-once’ mode. This is because
omloop is connected to two objects but contains a random function. We want to
make sure the same information is given to both the Chord-seq and the BPF, which will not happen
unless we ‘freeze’ it after one evaluation.
Now let’s look inside omloop.
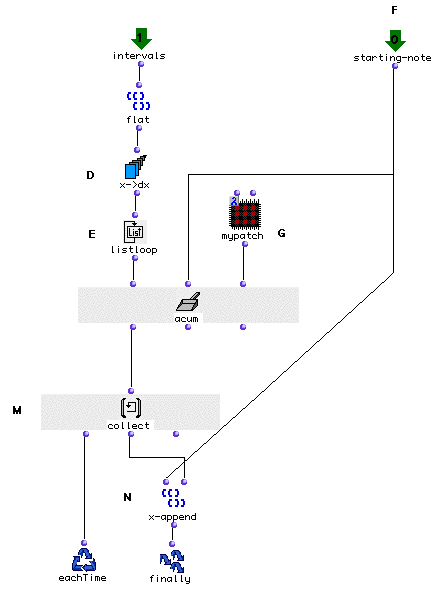
First of all we must convert the list of midics we will be receiving through
the _intervals_ input into a list of relative intervals. This is done, as
usual, using x->dx. We must first use flat
since the _lmidic_ output of the Chord-seq is a
nested listand x->dx needs a flat
list.
Each interval of the Chord-seq will thus be enumerated individually and passed to our lambda patch (G) along with the results of the previous calculation.
Here’s the lambda patch:
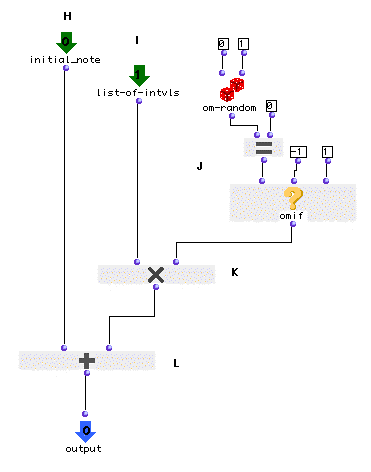
The lambda patch (G) will take the initial note (H) and will add to it the first interval (I). This interval will have been first multiplied either by 1 (which will leave it as is) or by -1 (which will invert the interval.)
In order to randomly invert the intervals we have used om-random. As we know, om-random returns random numbers
between limits set at its inputs. In our case we had to use a different
strategy because we are only interested in having -1 and 1. Simply using om-
random could have returned some zeroes. This is where
omif comes in handy. We used om-random with
0 and 1 as arguments and connected it to the predicate om=in
order to transform each zero into a -1. If om-random
returns a zero, om= will return t and omif,
in turn, will return -1. If not, 1 is returned.
Once we have added our first interval (using om+) to the
initial note, the result will be a new note which will take the place of the
old as the internal state of our acum collector. In
order to record each note we use collect, connected to the
first output of acum, as we did in the previous
tutorial.
Lastly, in order to have both factories (the BPF
and the Chord-seq) evaluated in a single evaluation we
will use sequence. sequence evaluates
all its arguments sequentially, but you will only see one in the Listener. For
instance, if we evaluate the first output of sequence we
will obtain the BPF object in the listener.
Evaluating the second output will return the Chord-seq
object. Both will be evaluated in the patch window, however.
Prev| Home| Next
—|—|—
Tutorial 36: Accumulation| Up| Flow Control IV:
Recursive Functions