OpenMusic Tutorials

Prev| Chapter 14. Flow Control IV: Recursive Functions| Next

Tutorial 38: Recursive patch I

Topics

Introduces the concept of recursion

Key Modules Used

omif, omloop, om=, om-

The Concept:

As we have seen, OM patches can contain calls to functions, factories, etc., nested to any level we like. It is even possible to put a call to itself within a function! A function which contains itself (created by dragging the patch from the Workspace into the patch window itself) is called a recursive function. Recursion is actually extremely useful and a powerful part of object-oriented programming.

Some computations require recursive functions, while others benefit from the clarity or speed of recursion, though they may be possible other ways. For example, the factorial procedure performed in Tutorial 36 can be performed more elegantly (and more quickly, it turns out) using a recursive function.

The scheme of the recursive function for finding 5! (5 factorial, that is the product 12345) for example, can be summarized:

First, we reverse our list: 54321
4 can be represented as (5-1). This means we start by mutiplying 5*(5-1).
3 can be represented as ((5-1) -1 ). So we multiply 5(5-1)((5-1) -1)Get the idea?.
The next level of recursion would be (((5-1) -1 ) -1), and so on, until we reach 1.

We can imagine a function that multiplies 5 by a value taken from its last repetition and passes that to itself along with the value to multiply by (minus one). And here we run into a problem- since recursive functions call themselves, they must have a built in ‘brake’ in the form of a termination test. Only if the termination test fails should they call themselves. Without a termination test, the function continues to call itself on into infinity, eventually saturating the available memory and causing an error:

`> Error: Stack overflow on control stack. > To globally increase stack space,

increase minimum-stack-overflow-size > While executing: “Unknown” > Type Command-/ to continue, Command-. to abort. > If continued: Continue with a larger stack See the Restarts menu item for further choices.`

Let’s look at a recursive patch in OM which will calculate the factorial of whatever number we give it:

The Patch:

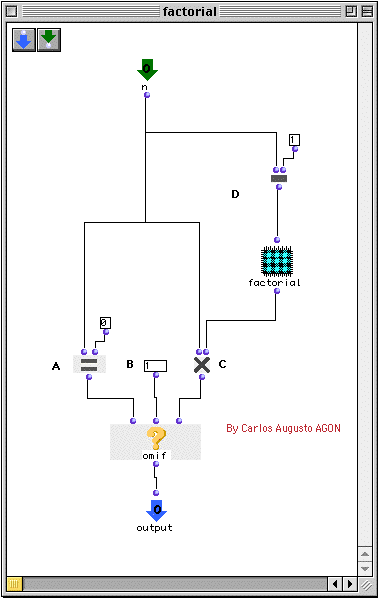
On the first repetition, _n_ is equal to 5 (in our example.) If _n_ is not equal to zero, which it is not, om* is called to multiply _n_ and the result of the recursion into the patch factorial. The trick is that we subtract 1 from _n_ before passing it to factorial. Before om* can complete, it must evaluate factorial. So factorial is evaluated using 4 for _n_. This recursion continues, going one level deeper each time (like Russian dolls), until finally, _n_ is zero. At this point, omif (the termination test at B) will return 1 instead of evaluating factorial. 1 is passed to the output, which (remember the Russian dolls?) is going to be coming into the om* function in the level of recursion just above. In that level, _n_ was equal to 1. 1 times 1 is 1, which is passed to the output, which is itself the second input to om* on the next level. _n_ is 2 on this level, and 2 times 1 is 2. Two is passed up out of that recursion to the next level where _n_ is 3. The product, 6, is passed, and we continue to work back up, layer by layer, until we reach the top, where the product of 12345, 120, is passed to the output.

To see this patch in action, drag it into any other patch.

Evaluate it with different numbers. Notice how it takes a longer time for big numbers (since more levels of recursion are being created).

OpenMusic