OpenMusic Tutorials

Prev| Chapter 14. Flow Control IV: Recursive Functions| Next

Tutorial 39: Recursive patch II

Topics

Using a recursive patch to reverse the output of a rhythm tree.

Key Modules Used

omif, Voice, standard LISP functions

The Concept:

As we saw in Tutorial 24, traditional rhythmic notation in the Voice object is formalized in what’s called a rhythm tree. The rhythm tree is a series of nested lists in the form (D S) where D is the duration and S is the structure of that duration, and S may contain additional lists in the form (D S). Notice that this form is itself recursive, containing the same element on many different structural levels. Taking a retrograde of such a structure is not equivalent to taking the retrograde of the rhythm it represents.

Consider this rhythm:

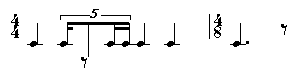
represented by the rhythm tree:

(? (((4 4) (1 (1 (1 -2 1 1)) 1 1)) ((4 8) (3 -1))))  

If we go through the list from beginning to end we will notice that in order to obtain a correct retrograge rhythm some expressions must be reversed and others not. For example, the first element ‘?’ must always figure in the beginning of the list and therefore must be left as is. Measure signatures must also figure in the beginning of each measure-list. In general, all elements in ‘D’ position of a rhythm tree must be left alone. Only ‘S’ elements must be reversed, such as the (1 -2 1 1), it being a low level rhtyhm structure representing a quintolet.

The correct retrograde form is thus:

(? (((4 8) (-1 3)) ((4 4) (1 1 (1 (1 1 -2 1)) 1))))  

Representing the notation:

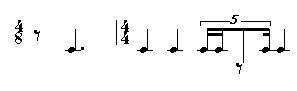
Notice that this is not what we get by putting the original tree through the LISP function reverse.

A rhythm tree can have unlimited levels of nesting. In addition, not all measures need have the same number of levels, so a simple omloop won’t do the trick. We must create a recursive function which calls itself as many times as necessary to descend the levels of recursion in the rhythm tree. For each element (D S), we will reverse S but leave D untouched.

The Patch:

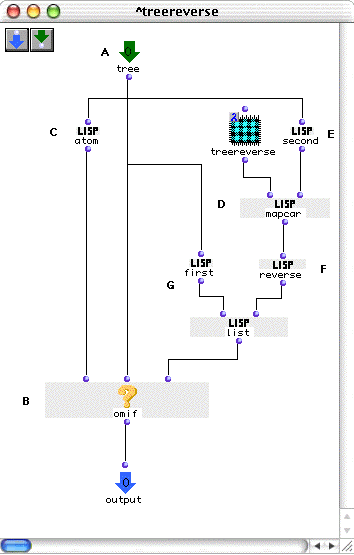
Here it is. The actual reversal of elements is accomplished by (E) and (G), which split the (D S) structure into its first and second elements and reverse the second.

The termination test is performed by omif using a special LISP predicate, atom, which returns t only if its input is not a list. Recursion will thus stop when we reach the “bottom” of the rhythm tree.

mapcar is used to call the recursive part of the patch. mapcar takes our treereverse and applies it to all sublists of the ‘S’ portion of the current level of the tree.

Once the termination test is satisfied and we begin to work back out of the levels of recursion, the reversed portions of the lists (the ‘S’ portion’) representing the distribution of rhythmic values will be put back together with the ‘D’ portions (the time signatures, which we didn’t touch) with the list function.

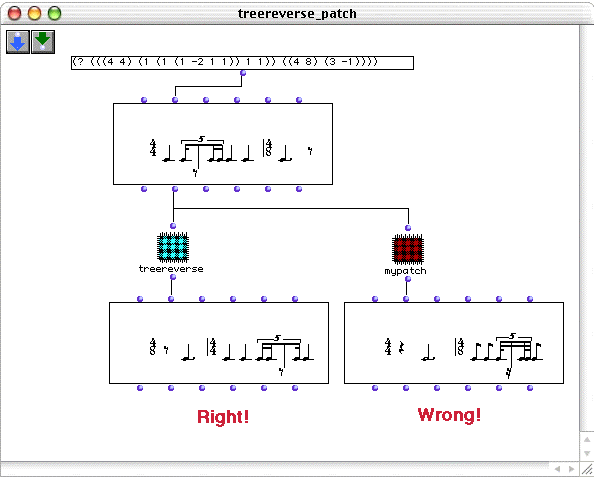
The result is the correct retrograde of the rhythm. To further prove our point about the necessity of the recursive function, let’s look at the incorrect results of a simple non-recursive function which splits the D and S elements apart and reverses the S elements.

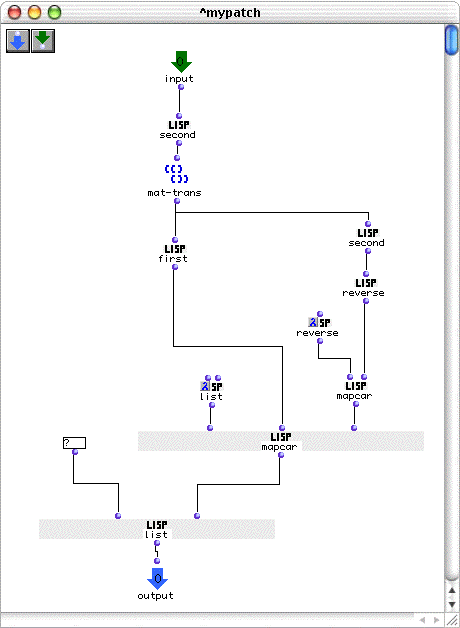
This patch has two problems. The first is that it only reverses elements down to two levels of rhythm-tree sublists. If we had smaller rhythmic values as groups within beats of the measures, they would not have been reversed.We don’t so this is not a problem. The second problem, and this one shows up, is that the order of time signatures is not reversed. See for yourself: