OpenMusic

Visual Programming | Computer-Assisted Composition

Navigation : Previous | Next

  Rhythm Trees in details

The Rhythm Tree format ( RT ) must be understood as an alternative in the description of symbolic rhythmical structures that allows a complete cohesion with  traditional to most complex musical notation. This format was issued from different attempts in rhythmical descriptions that have been explored in Patchwork and OpenMusic environments [1].

A.    The syntax

An RT is defined as a couple (D S) where

Here are some RTs that complies with the above syntax:

(1 (1 1 1 1))

a structure whose extent is, say, a whole-note (1), and which contains 4 equally lasting values, 4 quarter notes inthat case.

(2 ( (1 (1 1 1 1)) (1 (1 1 1 1)) )

a structure lasting two whole-notes, containing two equal substructures, each lasting a whole-note. These substructures in turn contain 4 equal values i.e. quarter notes. So it can be interpreted as a voice containing 2 measures in 4/4.

B.    The Semantics

For an RT = ( D S ), D expresses a temporal field (a duration).  S defines a group of proportions taking place in D. For example, for RT = (1 (1 1 1 1)) and the unit being the quarter note, the represented rhythm will be the following:

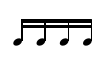
When the number D is at the level of a voice, it is by convention expressed in whole-note units.

When the number D is at the level of a measure, it is by convention expressed in whole-note units, and it may also be expressed by a ratio e.g.:

4/4, 7/8, 5/2

or a list e.g. :

(4 4) (7 8) (5 2)

which meaning is the usual musical one for time signature. Due to a specificity of the underlying Common Lisp system, ratios like 4/4 are automatically simplified (i.e. 4/4 = 1). In that case, the list form should be chosen (i.e. (4 4)) or , alternatively, he special notation 4//4.

To avoid tedious calculations, D can be replaced by a question-mark ‘?’. In that case OM will figure out the actual value of D. Our previous example can then be rewritten as :

(? ( (1 (1 1 1 1)) (1 (1 1 1 1)) )

The RT structure allows us to express in a most coherent manner different type of musical objects. Polyphonies, voices, measures, groups[3] are expressed as _RT_s.

By convention, when the value of D is on the measure level it will be expressed in a whole note unit[4]. For example, if we wish to express a measure of 3/4  containing three quarter notes, the RT will be:

((3 4)  (1  1  1))

As defined previously, S illustrates a set of proportions taking place in D. This is shown in the following example:

((4 4) (1   2     1))

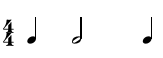
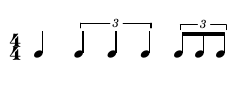
Up till now we have examined RTs where S was a set of simple elements (integers) that represented notes (pulses). In the following tree we will see more complex elements appearing in the place of S :

((4 4) (1 (2 (1 1 1)) (1 (1 1 1))))

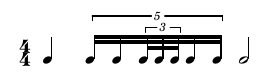
The RTs recursively contained in S represent what we will call groups. In general, groups are graphically represented as notes grouped by their stems. Alike measures, groups can also embed other groups as shown in the example below:

((4 4) (1 (1 ( 1 1 (1 (1 1 1)) 1 1)) 2))

We will extend the _RT_s syntax in order to incorporate rests and ties that will be respectively represented by negative integers and floats.

((4 4) (1 1.0  –1   1))

An RT expresses not only an absolute rhythm (proportional durations) but also its representation (symbolic representation). As we may observe below, the two rhythms being identical in proportion are different graphically (the second RT contains two groups):

((2 4) (2 2 2 2)) ((2 4) ((1(1 1))(1(1 1)))

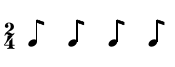
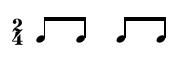
In some cases we might obtain syntactically correct RT_s with no traditional notational equivalency. Let us take for example the following _RT  ((5 4) (5)) that corresponds to the rhythm:

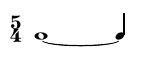
the associated RT is ((5 4) (4 1.0)). OpenMusic will automatically recalculate it as so for visualization.

Grace notes

Grace notes are expressed in the RTs as follows:

A single grace note is represented as a 0 integer:

(? (((4 4) (1 0 2 1))))

A group of grace notes will therefore be represented as an RT group where D is 0:

(? (((4 4) (1 (0 (1 1 1)) 2 1))))

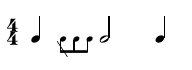
It is also possible to have a grace note before a rest as it is the case in this example:

(1 (((4 4) (1 0 -1 (1 (1 1 1)) 1))))

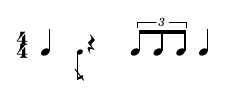
B.  Rhythm Trees and OpenMusic editors

In OpenMusic Rhythm Trees are used mostly with the VOICE object. There are many ways to write RTs . The straight forward way is to simply edit the VOICE’s second slot <tree> using either the popup numbox or even better, a textfile. In this case, don’t forget to remove the “outer” parenthesis

An even more practical and efficient way is to use the RT editor. First choose either voice or measure selector in your VOICE editor, then select the whole voice or a particular measure then type ‘r’

References

[1]    G. Assayag, C. Rueda, M. Laurson, C. Agon, and O. Delerue. “Computer assisted composition at Ircam: PatchWork & OpenMusic,” Computer Music Journal 23:3, 1999.

[2]    G. Cindy. “The notation interchange file format: a Windows compliant approach,” E. Selfridge-Field, ed. Beyond MIDI  - A Handbook of Musical Codes. Massachusetts : MIT Press. , 1997.

[3]    H. Hoos, K. A. Hamel, K. Renz, J. Kilian. “The GUIDO music notation format - a novel approach for adequately representing score-level music,” ICMC’98 Proceedings, p.451-454, Ann Arbor, 1998.

[4]    R. Mounce. “A brief discussion of standard music description language,” ISO/IEC Draft International Standard 10743, 1996.

[5]    B. Schottstaedt. “Common music notation,” E. Selfridge-Field, ed. Beyond MIDI  - A Handbook of Musical Codes. Massachusetts : MIT Press. , 1997.

Contents :

Navigation : Previous | Next